Apoyando una figura en un plano oblicuo

¡Hola discontinuos!

Hoy os traigo un nuevo ejercicio de sistemas de representación con el que repasaremos algunos conceptos de abatimiento y perpendicularidad en diédrico.

1.       Dadas las vistas de una pieza, se pide recomponer la figura tridimensional.

2.       Apoyar la figura sobre el plano inclinado dado en diédrico, sabiendo la arista del cubo se corresponde con el segmento AB perteneciente al plano.

AXONOMETRÍA. Esbozamos la solución a mano alzada en axonometría, por ejemplo, en isométrica y axonometría militar. Queremos un boceto rápido así que no nos preocuparemos de los coeficientes de reducción; abordaremos las peculiaridades del sistema axonométrico en posteriores entradas. 

DIÉDRICO. Abordaremos el problema comenzando por determinar la base de la figura sobre el plano dado. Para obtener la proyección horizontal del segmento AB, debemos recordar algunos conceptos de pertenencia. En el modelo de Monge, decimos que una recta pertenece a un plano cuando sus trazas están contenidas en las trazas del plano. Las trazas del plano no son más que dos rectas del mismo, en concreto la intersección con los planos de proyección; las trazas de la recta son, de igual modo, dos puntos particulares de ella (su intersección con los planos de proyección). Podemos, por tanto, generalizar diciendo que una recta pertenece al plano cuando interseca con dos rectas del mismo, o lo que es igual, cuando comparte 2 puntos con el plano.

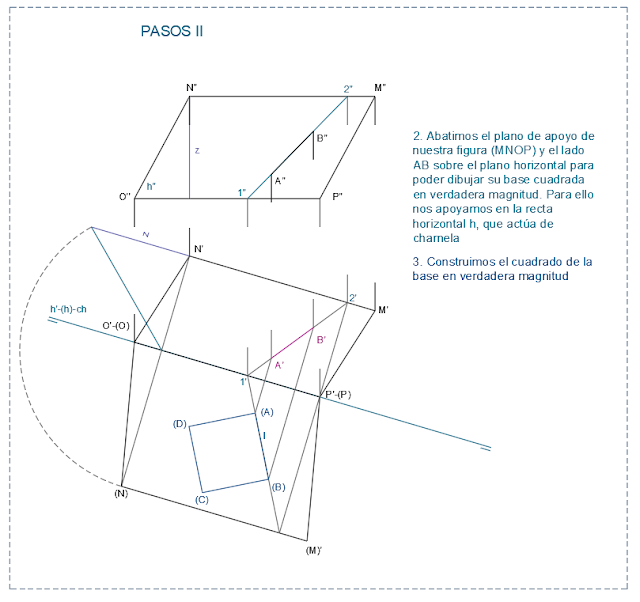
Pero..., ¿cómo completamos la base de la figura? Sabemos que nuestra figura tiene base cuadrada, por tanto, conocemos su forma en verdadera magnitud. Nos podemos apoyar en un abatimiento sobre un plano horizontal para obtenerla. Recordemos el concepto de abatimiento sobre el boceto tridimensional: 

Queremos abatir α sobre un plano horizontal cualquiera H. Por tanto, tomamos como eje de abatimiento una recta horizontal de α, por ejemplo, h, (que no es más que la intersección de α con H).

Y ahora, ¿cómo hallamos la hipotenusa del triángulo IN’N? Fácil. Sabemos la altura de N con respecto a h (z) y también su alejamiento. Además, sabemos que la proyección de un punto (N’) y su abatido (N) están sobre una recta perpendicular al eje de abatimiento o charnela. Tenemos todos los datos necesarios para abatir AB y dibujar el cuadrado de la base en verdadera magnitud:

A continuación, desabatimos apoyándonos en rectas auxiliares y sabiendo que, en diédrico, por ser una proyección cilíndrica ortogonal, rectas paralelas en el modelo tridimensional se proyectan paralelas:

Para continuar la construcción necesitamos recurrir al concepto de perpendicularidad. La altura del cubo es perpendicular al plano sobre el que apoya. De acuerdo con el teorema de las tres perpendiculares, una recta es perpendicular a un plano si lo es a dos rectas no paralelas contenidas en dicho plano. Además, una recta perpendicular a un plano es perpendicular a sus trazas, es decir, a la intersección de dicho plano con los planos de proyección. Al estar trabajando en diédrico directo no tenemos propiamente trazas, pero, sí sabemos su dirección: Las rectas horizontales y frontales son paralelas a las trazas del plano, (son la intersección del plano oblicuo con planos paralelos a los planos de proyección). Ya tenemos rectas horizontales, trazamos una frontal por pertenencia y hallamos perpendiculares a sus proyecciones horizontal y frontal respectivamente.

Ahora, ¿cómo obtenemos la dimensión de las aristas perpendiculares al plano en proyección horizontal y vertical? Sabemos su dimensión en verdadera magnitud, lado l del cubo, por tanto, acudimos a un triángulo rectángulo y tales para resolver:

Ya solo falta completar la cara superior del cubo (por paralelismo), inscribir la figura y determinar partes vistas y ocultas.

¡Problema resuelto!