Curvas cónicas: hipérbola y tangentes

 Seguimos estudiando las curvas cónicas, esta vez aplicando los conceptos a la determinación de tangentes y elementos de una hipérbola. El problema es…

Dada una hipérbola por sus asíntotas y un foco determinar una circunferencia focal, la circunferencia principal, los vértices de la curva y la tangente desde el punto exterior R.

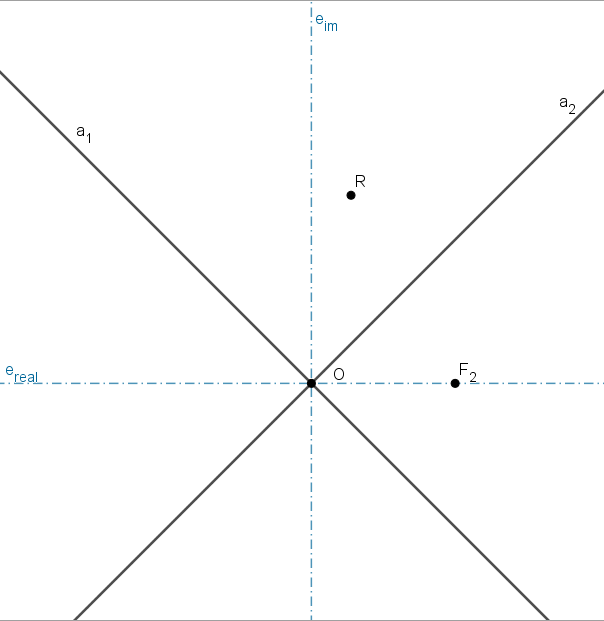enunciado

¿Sabes resolverlo? ¡Comprueba la solución pinchando en los  botones del siguiente Geogebra!

PROCEDIMIENTO

Determinación del foco F₁: es simétrico del foco F₂ con respecto al eje imaginario.

Circunferencia focal 1: Es el lugar geométrico de los simétricos del foco contrario respecto de las tangentes a la hipérbola. Por tanto, como las asíntotas son las tangentes a la curva en el infinito, bastará con hallar el simétrico de F₂ respecto de a₂. Trazamos la circunferencia con centro en F1 y radio F1-F2’, focal buscada.

Circunferencia principal o lugar geométrico de los pies de las perpendiculares a las tangentes trazadas desde los focos. El pie de la perpendicular sobre la asíntota P determina un punto de la circunferencia; con centro en O completamos su trazado.

Vértices: son la intersección de la circunferencia principal con el eje real.

Tangentes desde R: de forma análoga a lo realizado en el caso de la elipse y la parábola, partimos de la definición de la circunferencia focal. Esta contendrá a los simétricos de los focos respecto de las tangentes buscadas. Además, dichos simétricos estarán a igual distancia que el foco de R (por la simetría de la que son partícipes). Trazamos una circunferencia con centro en R y radio RF₂. La intersección de ambas circunferencias determina los simétricos de los focos. Las tangentes son las mediatrices de los segmentos de F₂’’F₂ y F₂’’’F₂. Los puntos de tangencia se encuentran en la intersección de las tangentes con las rectas de unión de los simétricos de F₂ y el foco contrario F₁